Cách tính lỗi bình phương trung bình (MSE) trong Microsoft Excel

Trong thống kê, sai số bình phương trung bình (MSE) là một số liệu quan trọng đo lường mức độ sai sót trong mô hình thống kê. Nó thường được dùng để đánh giá độ chính xác của một mô hình dùng để dự đoán các giá trị trong tương lai.

Trong hướng dẫn này, chúng tôi sẽ giải thích MSE chi tiết hơn và sau đó chỉ cho bạn cách tính MSE trong Excel.

Lỗi bình phương trung bình là gì?

Sai số bình phương trung bình (MSE) là phép tính đo lường chênh lệch bình phương trung bình giữa giá trị ước tính và giá trị thực tế trong tập dữ liệu. Nói cách khác, nó ước tính mức độ sai sót trong một mô hình thống kê. Đối với những người đam mê thống kê, nó tính toán mức độ phù hợp của đường hồi quy với một tập hợp các điểm dữ liệu.

Ví dụ: giả sử bạn có một mô hình dự đoán giá trị doanh thu mà bạn sẽ nhận được với tư cách là một công ty phần mềm trong một năm. Vào cuối năm, bạn nhập giá trị bán hàng thực tế mà bạn đã tạo ra. Sau đó, bạn có thể tính toán MSE để xem mô hình của bạn dự đoán kết quả tốt đến mức nào.

MSE được tính bằng cách lấy trung bình của các chênh lệch bình phương giữa giá trị dự đoán và giá trị thực tế của biến mục tiêu.

Công thức MSE trông như thế này:

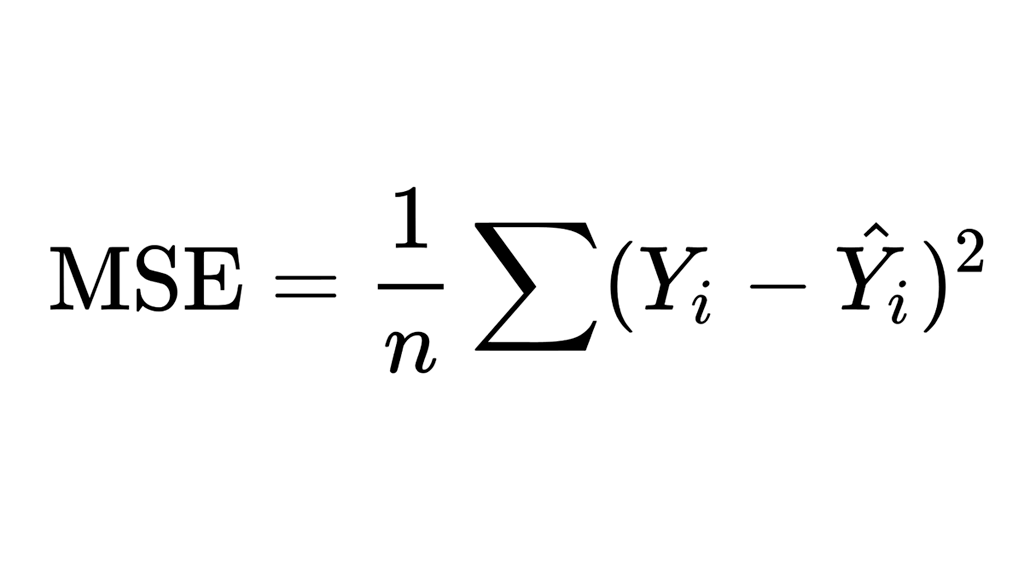
Ở đâu:

Σcó nghĩa là tổng các giá trị;

nlà cỡ mẫu hoặc số lượng quan sát;

Yilà các giá trị được quan sát và;

Ŷilà các giá trị được dự đoán.

Giá trị lỗi thấp hơn cho biết mô hình có sai số chuẩn nhỏ hơn và dự đoán biến mục tiêu tốt hơn. MSE được sử dụng rộng rãi trong hồi quy thống kê và phân tích dữ liệu, đồng thời có thể hữu ích trong việc so sánh các mô hình hoặc điều chỉnh tham số khác nhau nhằm cải thiện độ chính xác của dự đoán.

Điều này có vẻ khó hiểu nhưng không quá khó để theo dõi khi chúng tôi chia nhỏ nó thành các phần sau.

Cách tính sai số bình phương trung bình trong Microsoft Excel

Có hai cách chính để bạn có thể tính toán MSE trong Microsoft Excel: hàm SUMSQ, hàm TRUNG BÌNH và công thức MSE. Chúng tôi sẽ sử dụng ví dụ bên dưới để chỉ cho bạn cách tính MSE bằng từng hàm sau:

Trong ví dụ đơn giản này, chúng ta sẽ xem xét giá trị doanh số hư cấu cho mỗi tháng (Cột A). Các giá trị ước tính được trình bày ở Cột B và các giá trị thực tế ở Cột C..

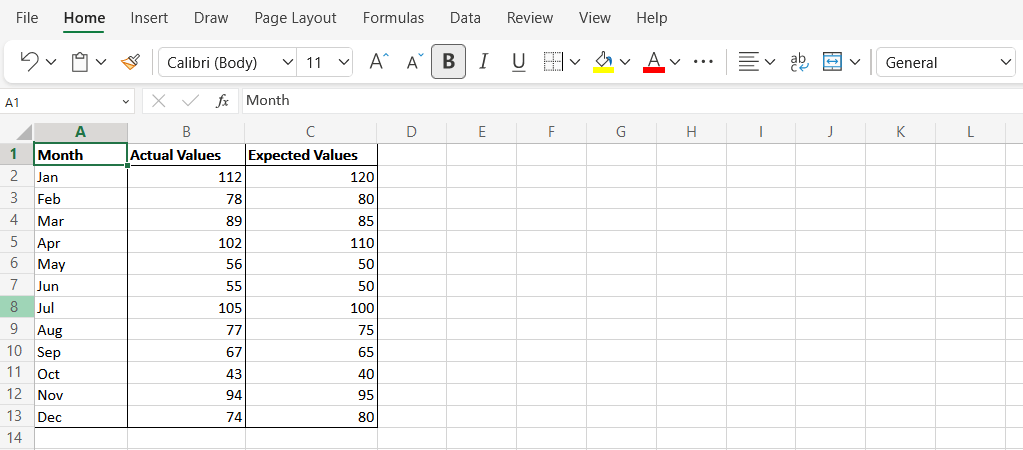
Tính MSE bằng hàm SUMSQ

Hàm SUMSQ trong Excel được sử dụng để tính tổng các bình phương của các số trong một phạm vi. Đây là cách sử dụng nó để tính toán MSE:

Tạo một cột mới trong Cột D có tên là “Sự khác biệt”. Điều này sẽ thể hiện sự khác biệt giữa giá trị dự kiến ​​và giá trị thực tế.

Sử dụng công thức “C2-B2” để tính chênh lệch cho các điểm dữ liệu trong mỗi hàng.

Chọn một ô mới và nhập cú pháp sau: “=SUMSQ(D2:D13/COUNT(D2:D13)”. Thay thế các ô trong công thức bằng các ô chính xác từ bảng tính Excel của bạn. Kết quả cuối cùng trong ô này là MSE của bạn.

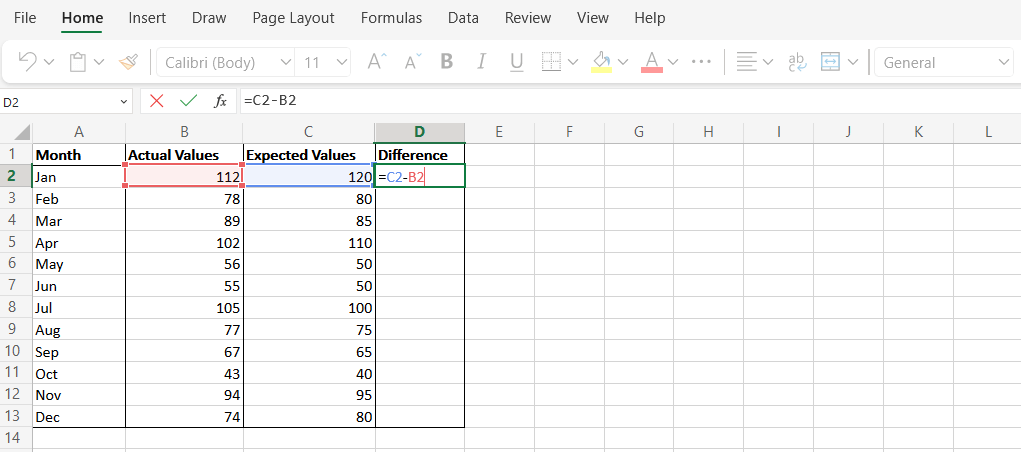
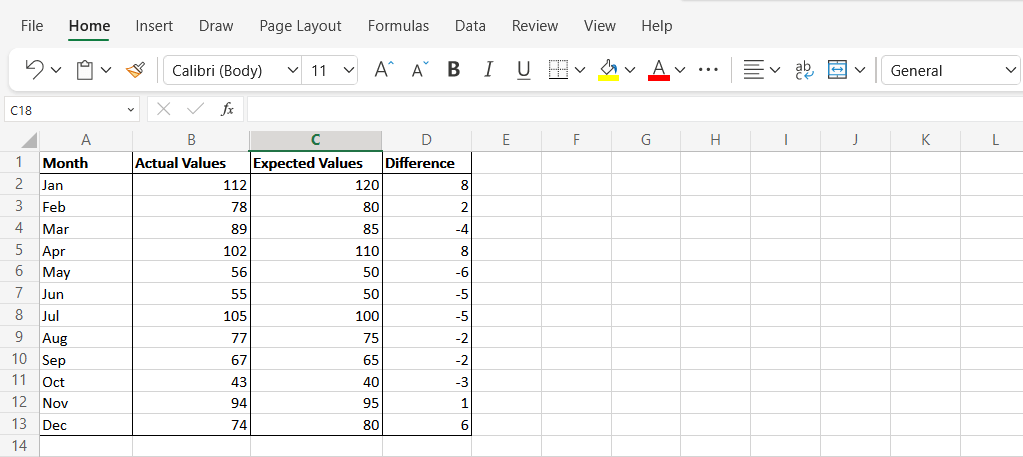
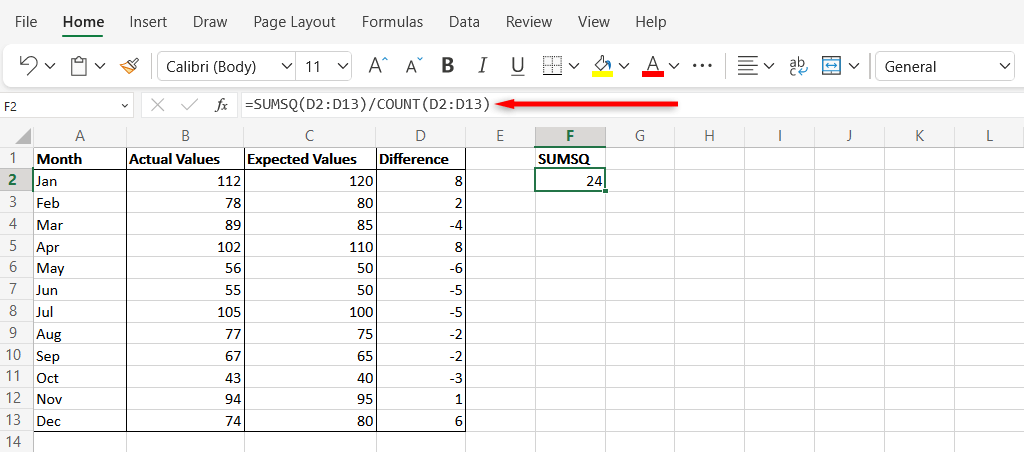
Tính MSE bằng hàm AVERAGE

Hàm AVERAGE trong MS Excel dùng để tính trung bình cộng của một dãy số. Phương thức này trả về kết quả giống như hàm SUMSQ nhưng mỗi bước được thực hiện thủ công.

Thực hiện Bước 1 và 2 được mô tả trong phương pháp SUMSQ. Điều này sẽ trả về sự khác biệt giữa giá trị dự báo và dữ liệu thực tế.

Đặt tên Cột E “Bình phương chênh lệch”, sau đó sử dụng công thức “=D2^2” để tính bình phương hiệu của từng giá trị trong Cột D.

Chọn một ô mới và tính giá trị trung bình của Cột E. Điều này sẽ trả về giá trị trung bình của các giá trị bình phương mà bạn đã tính toán trước đó. Để làm như vậy, hãy nhập “=AVERAGE(E2:E12)” và nhấn Enter. Đảm bảo thay thế các ô bằng các ô bạn đã sử dụng trong bảng tính của mình. Giá trị dữ liệu thu được là MSE của bạn.

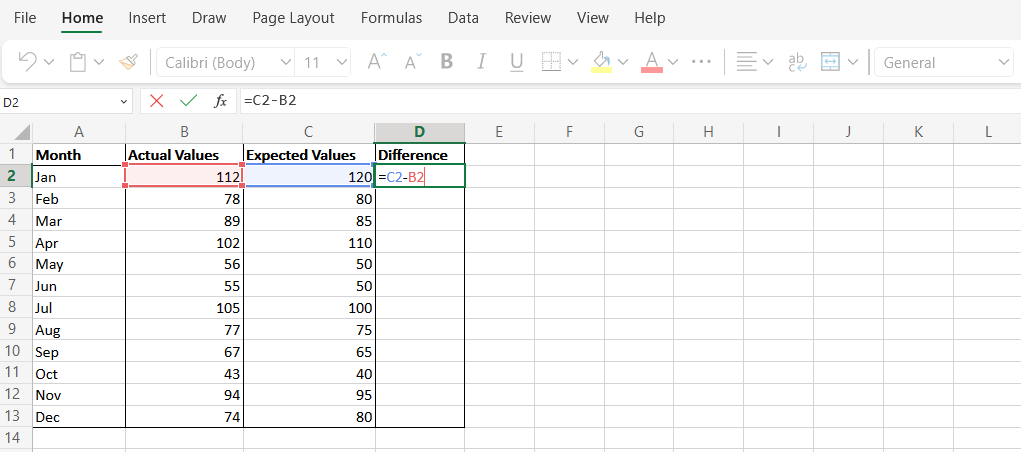
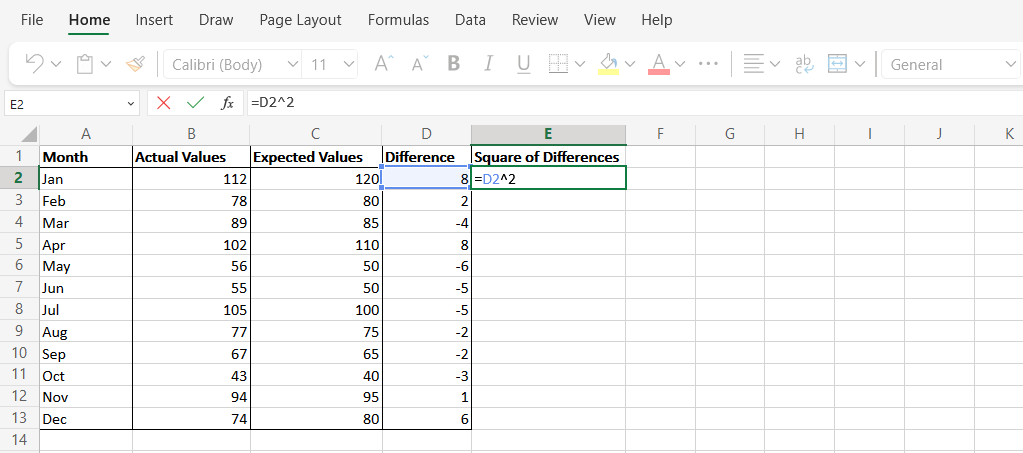
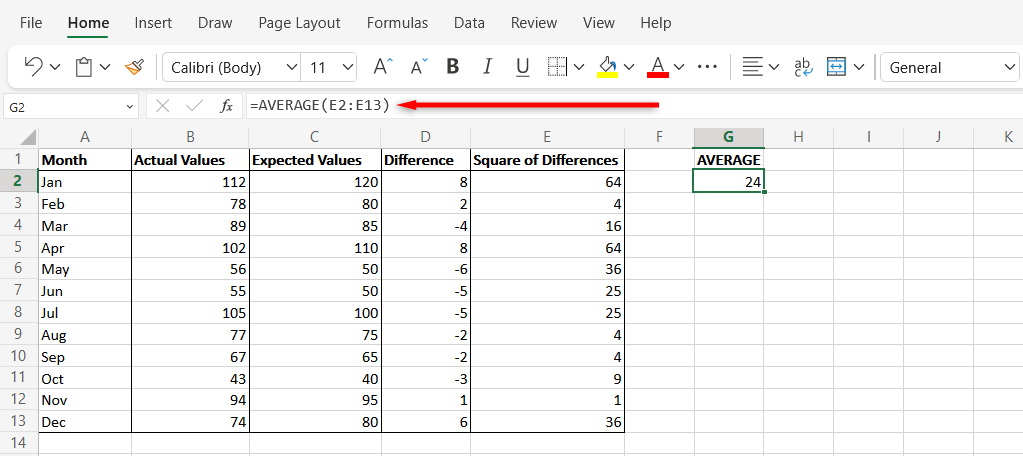
Phân tích thống kê trong Microsoft Excel

Microsoft Excel từ lâu đã là một trong những công cụ mạnh mẽ nhất để phân tích dữ liệu. Hy vọng với hướng dẫn này, giờ đây bạn có thể sử dụng Excel để tính MSE một cách dễ dàng. Và vì chúng rất giống nhau nên bạn có thể thực hiện các phép tính tương tự trong Google Trang tính.

.

bài viết liên quan: